What is a Neuron in ML?

A neuron is a basic building block of neural networks. In this post we break down the different parts of a neuron, and discuss how they work with a practical real-world example.

Neurons in Simple Terms

In simplest terms a neuron can be thought of as a inidividual processing unit. One or more scalar inputs are provided to a neuron, the neuron processes those inputs and produces a single scalar output value.

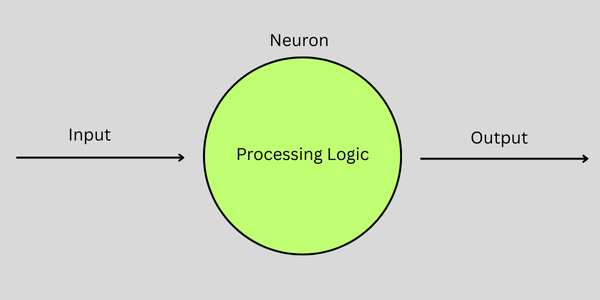
Technically this processing logic can be anything. In fact with a single input, a neuron could simply pass the input value through as output unchanged (e.g. input neurons, passthrough neurons). However a neuron's processing logic is usually more complex, and will include both "pre-activation" and "activation" functions which we discuss below.

Pre-activation Functions

A pre-activation function is applied to all of the (one or more) inputs passed to the neuron and returns a single scalar value. Generally this is a linear or affine function. A simple example of a pre-activation function is a sum of all inputs. This single summed value is then passed on to the activation function.

A Python example of this pre-activation function could look like this.

def preactivation(*inputs):
    return sum(inputs)

Activation Functions

An activation function produces a neuron's final scalar output. Generally an activation function is non-linear, which gives neural networks the ability to learn complex patterns and relationships within the data. A simple activation function could be a binary style step function where output is always a 0 or 1.

A Python example of this activation function could look something like this.

def activation(pre_activation_output):
    if pre_activation_output > 0:
        return 1
    else:
        return 0

Weights and Bias

When working with neurons you will often see the terms "weights" and "bias". These are technically not part of the neuron, but are still helpful to understand.

Weights are used to control the impact of each input on the final output. So if we have 3 inputs, we will also have 3 weights. The neuron will then use these 3 inputs and 3 weights in its pre-activation function.

Bias is a single value also used in the pre-activation function. Generally this value is added as a last step in the pre-activation function.

A Practical Example

Let's close out this post with a more practical example of how nuerons are used. We will use 3 input values, weights, and a bias in this example.

Our pre-activtion function will be a "weighted sum", where we multiply each input value by its corresponding weight and sum the values. We will add the bias to our weighted sum.

Our activation function will run on our pre-activatation output. There are a variety of common activation functions to choose from. For this example we will use ReLU which will take the maximum of 0 and the pre-activation output.

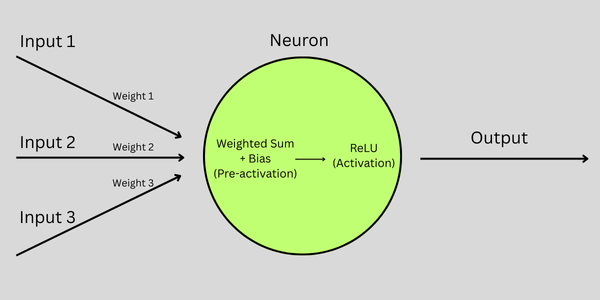
The Python version of this logic could look like this.

def preactivation(inputs, weights, bias):
    # compute the weighted sum and add bias 
    weighted_sum = 0
    for i in range(len(inputs)):
        weighted_sum += inputs[i] * weights[i]
    weighted_sum += bias
    return weighted_sum

def activation(preactivation_output):
    # ReLU activation function
    return max(0, preactivation_output)

# example values
inputs = [1.0, -2.0, 3.0]
weights = [0.5, 0.25, -1.0]
bias = 0.1

# compute pre-activation output
preactivation_output = preactivation(inputs, weights, bias)
print(f"Pre-activation output: {preactivation_output}")

# apply ReLU activation
activation_output = activation(preactivation_output)
print(f"Neuron output (ReLU): {activation_output}")

When using mathematical expressions, often inputs will shown as x, weights will be shown as w, and bias will be shown as b. So our example above would look like this.